Marvin F. da Silva, Felix Dangel, Sageev Oore

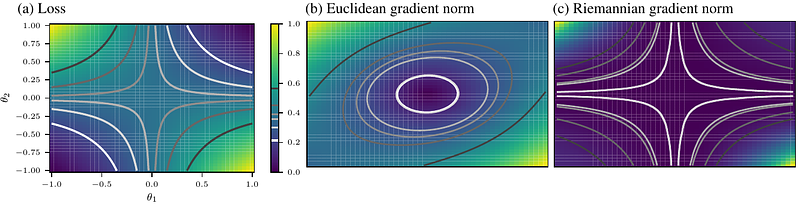
The concept of sharpness has been successfully applied to traditional architectures like MLPs and CNNs to predict their generalization. For transformers, however, recent work reported weak correlation between flatness and generalization. We argue that existing sharpness measures fail for transformers, because they have much richer symmetries in their attention mechanism that induce directions in parameter space along which the network or its loss remain identical. We posit that sharpness must account fully for these symmetries, and thus we redefine it on a quotient manifold that results from quotienting out the transformer symmetries, thereby removing their ambiguities. Leveraging tools from Riemannian geometry, we propose a fully general notion of sharpness, in terms of a geodesic ball on the symmetry-corrected quotient manifold. In practice, we need to resort to approximating the geodesics. Doing so up to first order yields existing adaptive sharpness measures, and we demonstrate that including higher-order terms is crucial to recover correlation with generalization. We present results on diagonal networks with synthetic data, and show that our geodesic sharpness reveals strong correlation for real-world transformers on both text and image classification tasks.