Shinde, S.; Raju, A.

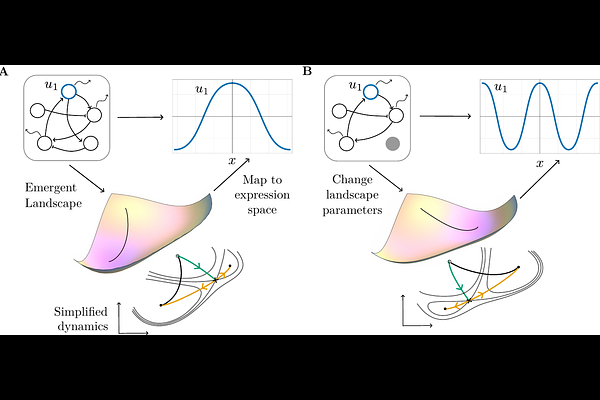
Turing patterns are a well-studied model of reaction-diffusion equations for developmental patterning. Their applicability has often been limited by the difficulty in identifying candidate molecules that satisfy the requisite criteria for patterning. Here, we build on recent work on geometric models to describe Turing patterning as a potential flow. We use the mathematics of normal form theory to capture the universal dynamics of Turing patterning, largely independent of the underlying reaction-diffusion equations. We apply our framework to three-component systems and demonstrate that we can accurately capture the dynamics of any given component. We extend our framework to larger networks and to models of Turing patterns coupled with external morphogens that provide positional information. Our normal form equations constitute a quantitative description of the dynamics of chosen markers, and we apply them to the dynamics of SOX9 expression during digit patterning.