Sakamoto, T.; Yeaman, S.

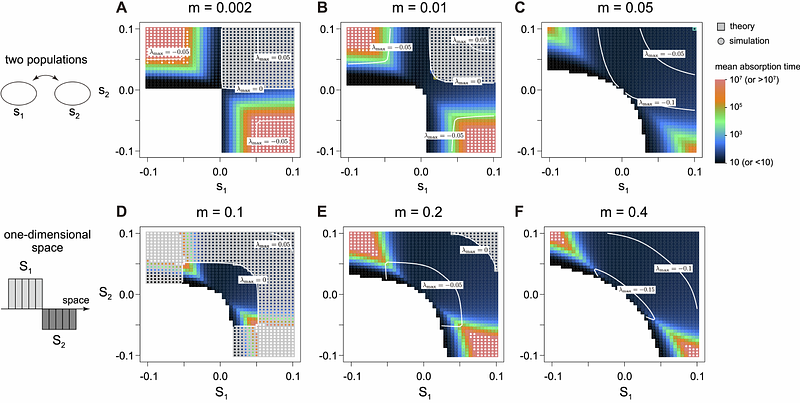
Local adaptation occurs when species adapt to spatially heterogeneous environments. The stability of local adaptation is determined by selection-migration-drift balance: selection favours adaptive divergence whereas migration and random genetic drift cause the collapse of the divergence. How this balance determines the dynamics of local adaptation has been extensively studied. However, owing to the complexity of multi-population models, most previous theories used models with simple population structure and environmental variation, limiting their applicability to complex situations in nature. To address this issue, we developed a new theoretical method to analyze complex multi-population models, allowing heterogeneity in selection, migration, and population density. In essence, our method approximates a spatial model by a panmictic one-population model while retaining the core stochastic structure, enabling the application of conventional diffusion methods. By comparing with simulations, we confirmed that our method accurately describes stochastic evolutionary dynamics in various spatial models, provided sufficient levels of migration. This method is then applied to examine the effect of environmental distribution in 2D space. Assuming landscapes with different levels of the spatial autocorrelation of the environment, we found that the maintenance of locally adaptive alleles is significantly promoted when the spatial autocorrelation is high. These results highlight how complex spatial heterogeneity, as seen in nature, could affect the qualitative outcome of evolution.