Sale, E.; Zhang, W.

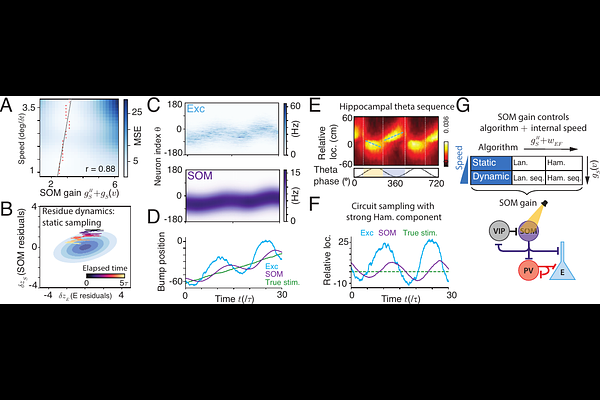
The brain lives in an ever-changing world and needs to infer the dynamic evolution of latent states from noisy sensory inputs. Exploring how canonical recurrent neural circuits in the brain realize dynamic inference is a fundamental question in neuroscience. Nearly all existing studies on dynamic inference focus on deterministic algorithms, whereas cortical circuits are intrinsically stochastic, with accumulating evidence suggesting that they employ stochastic Bayesian sampling algorithms. Nevertheless, nearly all circuit sampling studies focused on static inference with fixed posterior over time instead of dynamic inference, leaving a gap between circuit sampling and dynamic inference. To bridge this gap, we study the sampling-based dynamic inference in a canonical recurrent circuit model with excitatory (E) neurons and two types of inhibitory interneurons: parvalbumin (PV) and somatostatin (SOM) neurons. We find that the canonical circuit unifies Langevin and Hamiltonian sampling to infer either static or dynamic latent states with various moving speeds. Remarkably, switching sampling algorithms and adjusting model's internal latent moving speed can be realized by modulating the gain of SOM neurons without changing synaptic weights. Moreover, when the circuit employs Hamiltonian sampling, its sampling trajectories oscillate around the true latent moving state, resembling the decoded spatial trajectories from hippocampal theta sequences. Our work provides overarching connections between the canonical circuit with diverse interneurons and sampling-based dynamic inference, deepening our understanding of the circuit implementation of Bayesian sampling.