Anarya Ray

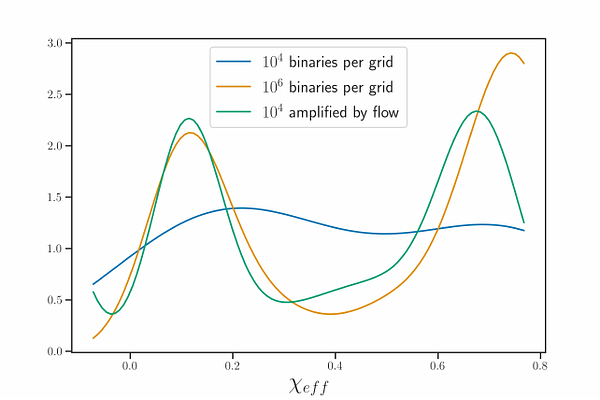
Population synthesis simulations of compact binary coalescences~(CBCs) play a crucial role in extracting astrophysical insights from an ensemble of gravitational wave~(GW) observations. However, realistic simulations are costly to implement for a dense grid of initial conditions. Normalizing flows can emulate the distribution functions of a simulated population of binary parameters and thereby enable empirical constraints on the astrophysical initial conditions and branching fractions of various formation channels given data from a catalog of GW observations. They can also be used for data amplification in sparse regions of the CBC parameter space to guide the development of phenomenological population models for rarely synthesizable systems with components in theorized mass gaps, without having to simulate a prohibitively large number of binaries. But flow predictions are wrought with uncertainties, especially for sparse training sets. In this work I develop a method for quantifying and marginalizing uncertainties in the emulators by introducing the Bayesian Normalizing flow, a conditional density estimator constructed from Bayesian neural networks. Using the exact likelihood function associated with density estimators I sample the posterior distribution of flow parameters with suitably chosen priors to quantify and marginalize over flow uncertainties. I demonstrate the accuracy, calibration, and data-amplification impacts of the estimated uncertainties for simulations of binary black hole populations formed through common envelope evolution. I outline applications of the methodology in simulation-based inference from growing GW catalogs and sketch other uses for general simulation-based approaches in GW astronomy.