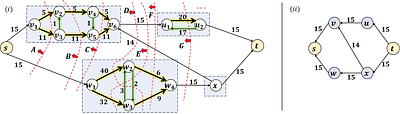
By: Deepak Ajwani, Rob H. Bisseling, Katrin Casel, Ümit V. Çatalyürek, Cédric Chevalier, Florian Chudigiewitsch, Marcelo Fonseca Faraj, Michael Fellows, Lars Gottesbüren, Tobias Heuer, George Karypis, Kamer Kaya, Jakub Lacki, Johannes Langguth, Xiaoye Sherry Li, Ruben Mayer, Johannes Meintrup, Yosuke Mizutani, François Pellegrini, Fabrizio Petrini, Frances Rosamond, Ilya Safro, Sebastian Schlag, Christian Schulz, Roohani Sharma, Darren Strash, Blair D. Sullivan, Bora Uçar, Albert-Jan Yzelman
By: Nick Fischer
By: Andreas Björklund, Petteri Kaski
By: Virginia Vassilevska Williams, Yinzhan Xu, Zixuan Xu
By: Surender Baswana, Koustav Bhanja
By: Hadley Black
By: Stephen Arndt, Josh Ascher, Kirk Pruhs
By: Calum MacRury, Will Ma
By: Jian Ding, Yumou Fei, Yuanzheng Wang
By: Jan Böker, Louis Härtel, Nina Runde, Tim Seppelt, Christoph Standke