We propose using Bayesian Persuasion as a tool for social media platforms to combat the spread of online misinformation. As platforms can predict the popularity and misinformation features of to-be-shared posts, and users are motivated to only share popular content, platforms can strategically reveal this informational advantage to persuade users to not share misinformed content. Our work mathematically characterizes the optimal information design scheme and the resulting utility when observations are not perfectly observed but arise from an imperfect classifier. Framing the optimization problem as a linear program, we give sufficient and necessary conditions on the classifier accuracy to ensure platform utility under optimal signaling is monotonically increasing and continuous. We next consider this interaction under a performative model, wherein platform intervention through signaling affects the content distribution in the future. We fully characterize the convergence and stability of optimal signaling under this performative process. Lastly, the broader scope of using information design to combat misinformation is discussed throughout. less

In this paper, we study a slightly different definition of popularity in bipartite graphs $G=(U,W,E)$ with two-sided preferences, when ties are present in the preference lists. This is motivated by the observation that if an agent $u$ is indifferent between his original partner $w$ in matching $M$ and his new partner $w'\ne w$ in matching $N$, then he may probably still prefer to stay with his original partner, as change requires effort, so he votes for $M$ in this case, instead of being indifferent. We show that this alternative definition of popularity, which we call weak-popularity allows us to guarantee the existence of such a matching and also to find a weakly-popular matching in polynomial-time that has size at least $\frac{3}{4}$ the size of the maximum weakly popular matching. We also show that this matching is at least $\frac{4}{5}$ times the size of the maximum (weakly) stable matching, so may provide a more desirable solution than the current best (and tight under certain assumptions) $\frac{2}{3}$-approximation for such a stable matching. We also show that unfortunately, finding a maximum size weakly popular matching is NP-hard, even with one-sided ties and that assuming some complexity theoretic assumptions, the $\frac{3}{4}$-approximation bound is tight. Then, we study a more general model than weak-popularity, where for each edge, we can specify independently for both endpoints the size of improvement the endpoint needs to vote in favor of a new matching $N$. We show that even in this more general model, a so-called $\gamma$-popular matching always exists and that the same positive results still hold. Finally, we define an other, stronger variant of popularity, called super-popularity, where even a weak improvement is enough to vote in favor of a new matching. We show that for this case, even the existence problem is NP-hard. less

In this paper, we present a model of a game among teams. Each team consists of a homogeneous population of agents. Agents within a team are cooperative while the teams compete with other teams. The dynamics and the costs are coupled through the empirical distribution (or the mean field) of the state of agents in each team. This mean-field is assumed to be observed by all agents. Agents have asymmetric information (also called a non-classical information structure). We propose a mean-field based refinement of the Team-Nash equilibrium of the game, which we call mean-field Markov perfect equilibrium (MF-MPE). We identify a dynamic programming decomposition to characterize MF-MPE. We then consider the case where each team has a large number of players and present a mean-field approximation which approximates the game among large-population teams as a game among infinite-population teams. We show that MF-MPE of the game among teams of infinite population is easier to compute and is an $\varepsilon$-approximate MF-MPE of the game among teams of finite population. less

Bilateral trade revolves around the challenge of facilitating transactions between two strategic agents -- a seller and a buyer -- both of whom have a private valuations for the item. We study the online version of the problem, in which at each time step a new seller and buyer arrive. The learner's task is to set a price for each agent, without any knowledge about their valuations. The sequence of sellers and buyers is chosen by an oblivious adversary. In this setting, known negative results rule out the possibility of designing algorithms with sublinear regret when the learner has to guarantee budget balance for each iteration. In this paper, we introduce the notion of global budget balance, which requires the agent to be budget balance only over the entire time horizon. By requiring global budget balance, we provide the first no-regret algorithms for bilateral trade with adversarial inputs under various feedback models. First, we show that in the full-feedback model the learner can guarantee $\tilde{O}(\sqrt{T})$ regret against the best fixed prices in hindsight, which is order-wise optimal. Then, in the case of partial feedback models, we provide an algorithm guaranteeing a $\tilde{O}(T^{3/4})$ regret upper bound with one-bit feedback, which we complement with a nearly-matching lower bound. Finally, we investigate how these results vary when measuring regret using an alternative benchmark. less

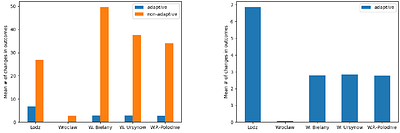
Participatory Budgeting (PB) is a form of participatory democracy in which citizens select a set of projects to be implemented, subject to a budget constraint. The Method of Equal Shares (MES), introduced in [18], is a simple iterative method for this task, which runs in polynomial time and satisfies a demanding proportionality axiom (Extended Justified Representation) in the setting of approval utilities. However, a downside of MES is that it is non-exhaustive: given an MES outcome, it may be possible to expand it by adding new projects without violating the budget constraint. To complete the outcome, the approach currently used in practice is as follows: given an instance with budget $b$, one searches for a budget $b'\ge b$ such that when MES is executed with budget $b'$, it produces a maximal feasible solution for $b$. The search is greedy, i.e., one has to execute MES from scratch for each value of $b'$. To avoid redundant computation, we introduce a variant of MES, which we call Adaptive Method of Equal Shares (AMES). Our method is budget-adaptive, in the sense that, given an outcome $W$ for a budget $b$ and a new budget $b'>b$, it can compute the outcome $W'$ for budget $b'$ by leveraging similarities between $W$ and $W'$. This eliminates the need to recompute solutions from scratch when increasing virtual budgets. Furthermore, AMES satisfies EJR in a certifiable way: given the output of our method, one can check in time $O(n\log n+mn)$ that it provides EJR (here, $n$ is the number of voters and $m$ is the number of projects). We evaluate the potential of AMES on real-world PB data, showing that small increases in budget typically require only minor modifications of the outcome. less

We study the allocation of shared resources over multiple rounds among competing agents, via a dynamic max-min fair (DMMF) mechanism: the good in each round is allocated to the requesting agent with the least number of allocations received to date. Previous work has shown that when an agent has i.i.d. values across rounds, then in the worst case, she can never get more than a constant strictly less than $1$ fraction of her ideal utility -- her highest achievable utility given her nominal share of resources. Moreover, an agent can achieve at least half her utility under carefully designed `pseudo-market' mechanisms, even though other agents may act in an arbitrary (possibly adversarial and collusive) manner. We show that this robustness guarantee also holds under the much simpler DMMF mechanism. More significantly, under mild assumptions on the value distribution, we show that DMMF in fact allows each agent to realize a $1 - o(1)$ fraction of her ideal utility, despite arbitrary behavior by other agents. We achieve this by characterizing the utility achieved under a richer space of strategies, wherein an agent can tune how aggressive to be in requesting the item. Our new strategies also allow us to handle settings where an agent's values are correlated across rounds, thereby allowing an adversary to predict and block her future values. We prove that again by tuning one's aggressiveness, an agent can guarantee $\Omega(\gamma)$ fraction of her ideal utility, where $\gamma\in [0, 1]$ is a parameter that quantifies dependence across rounds (with $\gamma = 1$ indicating full independence and lower values indicating more correlation). Finally, we extend our efficiency results to the case of reusable resources, where an agent might need to hold the item over multiple rounds to receive utility. less

When applied to question answering and other text generation tasks, language models (LMs) may be queried generatively (by sampling answers from their output distribution) or discriminatively (by using them to score or rank a set of candidate outputs). These procedures sometimes yield very different predictions. How do we reconcile mutually incompatible scoring procedures to obtain coherent LM predictions? We introduce a new, a training-free, game-theoretic procedure for language model decoding. Our approach casts language model decoding as a regularized imperfect-information sequential signaling game - which we term the CONSENSUS GAME - in which a GENERATOR seeks to communicate an abstract correctness parameter using natural language sentences to a DISCRIMINATOR. We develop computational procedures for finding approximate equilibria of this game, resulting in a decoding algorithm we call EQUILIBRIUM-RANKING. Applied to a large number of tasks (including reading comprehension, commonsense reasoning, mathematical problem-solving, and dialog), EQUILIBRIUM-RANKING consistently, and sometimes substantially, improves performance over existing LM decoding procedures - on multiple benchmarks, we observe that applying EQUILIBRIUM-RANKING to LLaMA-7B outperforms the much larger LLaMA-65B and PaLM-540B models. These results highlight the promise of game-theoretic tools for addressing fundamental challenges of truthfulness and consistency in LMs. less

We study the efficiency of non-truthful auctions for auto-bidders with both return on spend (ROS) and budget constraints. The efficiency of a mechanism is measured by the price of anarchy (PoA), which is the worst case ratio between the liquid welfare of any equilibrium and the optimal (possibly randomized) allocation. Our first main result is that the first-price auction (FPA) is optimal, among deterministic mechanisms, in this setting. Without any assumptions, the PoA of FPA is $n$ which we prove is tight for any deterministic mechanism. However, under a mild assumption that a bidder's value for any query does not exceed their total budget, we show that the PoA is at most $2$. This bound is also tight as it matches the optimal PoA without a budget constraint. We next analyze two randomized mechanisms: randomized FPA (rFPA) and "quasi-proportional" FPA. We prove two results that highlight the efficacy of randomization in this setting. First, we show that the PoA of rFPA for two bidders is at most $1.8$ without requiring any assumptions. This extends prior work which focused only on an ROS constraint. Second, we show that quasi-proportional FPA has a PoA of $2$ for any number of bidders, without any assumptions. Both of these bypass lower bounds in the deterministic setting. Finally, we study the setting where bidders are assumed to bid uniformly. We show that uniform bidding can be detrimental for efficiency in deterministic mechanisms while being beneficial for randomized mechanisms, which is in stark contrast with the settings without budget constraints. less

AI in Math deals with mathematics in a constructive manner so that reasoning becomes automated, less laborious, and less error-prone. For algorithms, the question becomes how to automate analyses for specific problems. For the first time, this work provides an automatic method for approximation analysis on a well-studied problem in theoretical computer science: computing approximate Nash equilibria in two-player games. We observe that such algorithms can be reformulated into a search-and-mix paradigm, which involves a search phase followed by a mixing phase. By doing so, we are able to fully automate the procedure of designing and analyzing the mixing phase. For example, we illustrate how to perform our method with a program to analyze the approximation bounds of all the algorithms in the literature. Same approximation bounds are computed without any hand-written proof. Our automatic method heavily relies on the LP-relaxation structure in approximate Nash equilibria. Since many approximation algorithms and online algorithms adopt the LP relaxation, our approach may be extended to automate the analysis of other algorithms. less

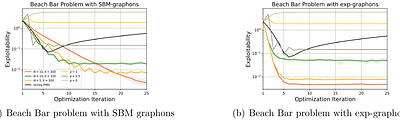
This paper studies two fundamental problems in regularized Graphon Mean-Field Games (GMFGs). First, we establish the existence of a Nash Equilibrium (NE) of any $\lambda$-regularized GMFG (for $\lambda\geq 0$). This result relies on weaker conditions than those in previous works for analyzing both unregularized GMFGs ($\lambda=0$) and $\lambda$-regularized MFGs, which are special cases of GMFGs. Second, we propose provably efficient algorithms to learn the NE in weakly monotone GMFGs, motivated by Lasry and Lions [2007]. Previous literature either only analyzed continuous-time algorithms or required extra conditions to analyze discrete-time algorithms. In contrast, we design a discrete-time algorithm and derive its convergence rate solely under weakly monotone conditions. Furthermore, we develop and analyze the action-value function estimation procedure during the online learning process, which is absent from algorithms for monotone GMFGs. This serves as a sub-module in our optimization algorithm. The efficiency of the designed algorithm is corroborated by empirical evaluations. less