Jennifer Rosina Andersson, Oleg Kochukhov, Zheng Zhao, Jens Sjölund

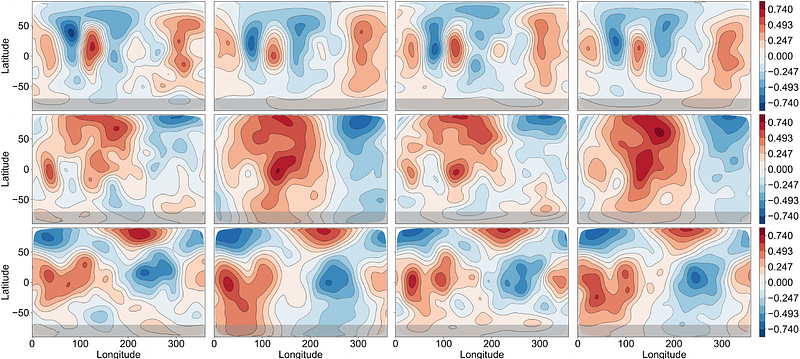
Zeeman-Doppler imaging (ZDI) is used to study the surface magnetic field topology of stars, based on high-resolution spectropolarimetric time series observations. Multiple ZDI inversions have been conducted for the early B-type star tau Sco, which has been found to exhibit a weak but complex non-dipolar surface magnetic field. The classical ZDI framework suffers from a significant limitation in that it provides little to no reliable uncertainty quantification for the reconstructed magnetic field maps, with essentially all published results being confined to point estimates. To fill this gap, we propose a Bayesian framework for probabilistic ZDI. Here, the proposed framework is demonstrated on tau Sco in the weak-field limit. We propose three distinct statistical models, and use archival ESPaDOnS high-resolution Stokes V observations to carry out the probabilistic magnetic inversion in closed form. The surface magnetic field is parameterised by a high-dimensional spherical-harmonic expansion. By comparing three different prior distributions over the latent variables in the spherical-harmonic decomposition, our results showcase the ZDI sensitivity to various hyperparameters. The mean magnetic field maps are qualitatively similar to previously published point estimates, but analysis of the magnetic energy distribution indicates high uncertainty and higher energy content at low angular degrees l. Our results effectively demonstrate that, for stars in the weak-field regime, reliable uncertainty quantification of recovered magnetic field maps can be obtained in closed form with natural assumptions on the statistical model. Future work will explore extending this framework beyond the weak-field approximation and incorporating prior uncertainty over multiple stellar parameters in more complex magnetic inversion problems.